Understanding major electronic components: an essential guide to analog and digital electronics

Introduction

Explore key electronic components, from their functions to practical applications, in this guide to analog and digital electronics. Discover how resistors, capacitors, inductors, diodes, transistors and LEDs contribute to technological evolution.

Electronics is a branch of applied physics that studies the control and manipulation of electrons to perform useful functions. This field has transformed the modern world, permeating every aspect of our daily lives, from communication devices to industrial automation systems, from medical devices to entertainment applications.

Electronics has origins that date back to the late 19th century with the discovery of the properties of the vacuum and the first vacuum tube devices, such as diodes and triodes. These devices were fundamental to the development of the first radios and communications systems. However, electronics as we know it today began to take shape in the 1940s with the invention of the transistor. This component revolutionized the field, allowing the miniaturization and increase in efficiency of electronic circuits.

As time passed, electronics evolved rapidly, leading to the creation of integrated circuits in the 1960s and 1970s. These devices contained thousands, and later millions, of transistors on a single silicon chip, paving the way for the modern era of computers and digital devices.

Analog and digital electronics

Electronics can be divided into two broad categories: analog and digital. Analog electronics concerns the manipulation of continuous signals that can take on an infinite number of values, such as the signal from a microphone or the video signal from a camera. Analog components, such as operational amplifiers, resistors, capacitors, and inductors, are used to process these signals.

On the other hand, digital electronics deals with discrete signals that take on only two values: 0 and 1. These signals are the basis of binary computing, used in all modern computers and digital devices. Digital circuits include components such as transistors, which operate like switches, and are organized into combinatorial and sequential logic to perform complex operations.

The fundamental building blocks of electronics, such as resistors, capacitors, inductors, diodes, transistors, and LEDs, are essential for building both analog and digital circuits. These components allow you to regulate, control and modify electrical signals to perform specific tasks. Understanding their operation and proper sizing is crucial for any circuit designer. Electronics is a vast and dynamic field, which continues to evolve with technological innovation. The transition from analogue to digital electronics has allowed the creation of increasingly complex and powerful devices, which are changing the way we live and work. Understanding the fundamental components and their uses is key to understanding and designing the electronic circuits that drive these innovations.

In this article we will examine how the following components work:

Resistors: limit the flow of current and divide voltages.

Capacitors: store electrical energy and filter signals.

Inductors: store magnetic energy and regulate current.

Diodes: allow the unidirectional flow of current.

Transistors: Amplify signals and act as switches.

LEDs: They emit light and are used as indicators.

The resistors

Resistors are essential components in any electronic circuit, designed to oppose the flow of electrical current. Made of various materials, including carbon slurry, metal oxide, and metal film, resistors come in many shapes and sizes, each suited to specific applications. Let us now highlight an important concept: the difference between resistor and resistance. Resistor is the physical component while resistance is a physical property that measures the ability of a material or component to oppose the flow of electric current. It is expressed in ohms (Ω) and depends on the nature of the material, its geometry and environmental conditions (such as temperature). Resistance is an inherent characteristic of materials and components, regardless of whether they are used in a specific resistor or other applications. The resistor is often indicated by the noun resistance. It is conceptually wrong but has now entered common technical language.

Let’s take an example to clarify the difference:

imagine a simple circuit consisting of a battery and a resistor:

• Resistor: the physical component in the circuit that has been designed and built to have a specific resistance. For example, a 10 Ω resistor.
• Resistance: the numerical value that describes how much the resistor opposes the flow of current. In this case, the resistance of the resistor is 10 Ω.

Another example with copper wire:

• Copper wire: a copper wire is not designed to be a resistor, but still has inherent resistance due to the properties of copper.
• Copper wire resistance: the resistance of copper wire depends on the length, diameter and temperature of the wire. Even though it is not a resistor, we can measure and calculate its resistance.

Structure and materials

Resistors are made of a resistive material that determines the value of the resistance, wrapped in a protective body often made of ceramic or plastic. Carbon film resistors, for example, consist of a carbon film laid on a ceramic cylinder, while metal film resistors use a thin layer of metal. Wire resistors, on the other hand, are wrapped with resistive wire on an insulating support.

Function and applications

The main function of resistors is to limit current, divide voltage, and dissipate energy in the form of heat. They are used in a wide range of circuits, including amplifiers, power supplies, timing circuits, and filters. In analog circuits, resistors can determine the gain of an amplifier, while in digital circuits they can be used for pull-ups or pull-downs to stabilize logic levels.

Color coding and tolerances

Resistors are identified by a color code that indicates their nominal value and tolerance. The color code is made up of colored bands, each representing a specific number and multiplier. For example, a resistor with brown, black, and red bands has a value of 1 kΩ. Additional bands can indicate tolerance, which is the maximum allowable variation from the nominal value. Common tolerances include 1% (brown), 5% (gold), and 10% (silver).

Color coding for three band plus tolerance resistors

The following table shows how to read the value of a resistor with three colored bands plus a tolerance band. Each color represents a specific number and multiplier, with an additional band for tolerance (which can be gold or silver). The resistor color code is read from left to right with the tolerance band to the right.

Color	First band	Second band	Multiplier	Tolerance
Black	0	0	×1	–
Brown	1	1	×10	± 1% (F)
Red	2	2	×100	± 2% (G)
Orange	3	3	×1,000	–
Yellow	4	4	×10,000	–
Green	5	5	×100,000	± 0.5% (D)
Blue	6	6	×1,000,000	± 0.25% (C)
Violet	7	7	×10,000,000	± 0.1% (B)
Gray	8	8	×100,000,000	± 0.05% (A)
White	9	9	×1,000,000,000	–
Gold	–	–	×0.1	± 5% (J)
Silver	–	–	×0.01	± 10% (K)
None	–	–	–	± 20% (M)

Suppose we have a resistor with the colored bands red, violet, orange and gold:

1. First band (Red): 2
2. Second band (Violet): 7
3. Multiplier (Orange): ×1,000
4. Tolerance (Gold): ± 5%

So, the value of the resistor is 27×1000= 27000 ohm (27 kΩ) with a tolerance of ± 5%.

Note:

The tolerance band is optional and may be absent. In this case, the tolerance is generally ±20%.

• Black, brown, and red colors are common for the multiplier in smaller resistance values, while gold and silver are used for fractions of ohms.

Color coding for four band plus tolerance resistors

There are resistors with a four-band color code plus a tolerance band. This type of color coding is common and includes three bands for significant values ​​and a fourth band for the multiplier, followed by the tolerance band. Here’s how to interpret these bands:

First three bands (nominal value):

1. First band: indicates the first significant digit.
2. Second band: indicates the second significant digit.
3. Third band: indicates the third significant digit.

Fourth band (Multiplier):

• Determine how many powers of ten the value should be multiplied by.

Tolerance band:

• Indicates the precision of the resistor value.

Color chart

Color	First band	Second band	Third band	Multiplier	Tolerance
Black	0	0	0	×1	–
Brown	1	1	1	×10	± 1%
Red	2	2	2	×100	± 2%
Orange	3	3	3	×1,000	–
Yellow	4	4	4	×10,000	–
Green	5	5	5	×100,000	± 0.5%
Blue	6	6	6	×1,000,000	± 0.25%
Violet	7	7	7	×10,000,000	± 0.1%
Gray	8	8	8	×100,000,000	± 0.05%
White	9	9	9	×1,000,000,000	–
Gold	–	–	–	×0.1	± 5%
Silver	–	–	–	×0.01	± 10%
None	–	–	–	–	± 20%

Reading example

Suppose we have a resistor with the colored bands brown, black, red, red and gold:

1. First band (Brown): 1
2. Second band (Black): 0
3. Third band (Red): 2
4. Multiplier (Red): ×100
5. Tolerance (Gold): ± 5%

So, the resistor value is 102×100 Ω=10200 Ω (10.2 kΩ) with a tolerance of ± 5%.

Power dissipated

The power dissipated by a resistor, measured in watts (W), is another crucial parameter. It is determined by the formula:

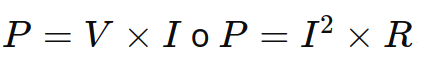
where P is the power, V is the voltage across the resistor and I is the current flowing through it. It is essential to choose a resistor with an adequate power rating to avoid overheating and damage. Standard resistors range from fractions of a watt to several watts, with high-power resistors can dissipate tens of watts (ceramic body resistors or even armored resistors).

Types of resistors

1. Carbon film resistors: inexpensive and used in general applications.
2. Metal film resistors: more precise and stable, used in circuits where high precision is required.
3. Wire resistors: used in high-power, high-precision applications.
4. Variable resistors (potentiometers): allow you to manually adjust the resistance, useful in volume controls and voltage regulators.

In summary, resistors are critical for controlling and regulating current in electronic circuits. Understanding materials, construction, color coding, tolerances, and power dissipation is essential to correctly selecting and sizing resistors for specific applications.

Ohm’s Law

Ohm’s law is one of the fundamental laws of electricity, describing the relationship between voltage (V), current (I), and resistance (R) in an electrical circuit. Ohm’s law is expressed by the formula:

Where:

• V is the voltage in volts (V)
• I is the current in amperes (A)
• R is the resistance in ohms (Ω)

Application of Ohm’s Law to a resistor

Suppose we have a simple circuit consisting of a battery and a resistor. We want to determine the current that flows through the resistor when it is connected to a 12 volt battery and has a resistance of 4 ohms.

1. Known data
   • Voltage V = 12V
   • Resistance R = 4 Ω
2. Ohm’s Law formula: V=I×R
3. Resolution for current I: I=V / R
4. Calculation: I = 12V / 4Ω = 3A

So, the current flowing through the resistor is 3 amps.

Check the power dissipated by the resistor

The power dissipated by a resistor can be calculated using the formula:

P=V × I

Where:

• P is the power in watts (W)
• V is the voltage in volts (V)
• I is the current in amperes (A)

Using the previously calculated values: P= 12 V×3 A = 36 W

Thus, the resistor dissipates 36 watts of power as heat.

This example shows how Ohm’s law can be applied to determine the current in a circuit and to calculate the power dissipated by a resistor.

Example: two resistors in series with a battery

Let’s consider a simple circuit where two resistors of different values ​​are connected in series with a battery. This example will demonstrate how to calculate the circulating current and voltages across resistors, illustrating the operation of a voltage divider. Furthermore, we will show a special case where the resistors have the same value and the battery voltage divides exactly in half.

Circuit data

• Battery: 12V
• Resistor R1: 4Ω
• Resistor R2: 8Ω

Calculation of the circulating current

In a series circuit, the current is the same in all components. The total resistance R_tot of the circuit is the sum of the individual resistances:

Using Ohm’s law to find the current I:

Therefore, the current circulating in the circuit is 1 ampere.

Calculation of the voltages across the resistors

The voltage across each resistor can be calculated using Ohm’s law. For resistor R1:

For resistor R2:

Therefore, the voltage across resistor R1 is 4V and across resistor R2 is 8V. We note that the sum of the voltages across the resistors is equal to the battery voltage:

Operation of the voltage divider

In a voltage divider, the total voltage is divided between the resistors in proportion to their resistance values. In our example, the 12V voltage split into 4V and 8V across R1 and R2 respectively, proportionally to the resistance values.

Special case: resistors of equal value

Let us now consider a particular case in which the two resistors have the same value:

• Resistor R1: 6Ω
• Resistor R2: 6Ω

The total resistance R_tot ​ is:

The current in the circuit is:

The voltage across each resistor is:

For R1:

For R2:

So, the voltage across each resistor is 6V. This shows that when two resistors of equal value are connected in series, the battery voltage is split exactly in half between the two resistors. This is a classic example of a voltage divider, where the output voltage depends on the values ​​of the resistors.

In summary, we have seen how to calculate the current and voltages in a circuit with resistors in series, illustrating both the operation of a voltage divider and the particular case of resistors with equal values.

Calculation of the overall resistance value

Resistors in series

When resistors are connected in series, the total resistance of the circuit is the sum of the individual resistances. This setup is simple and straightforward.

General formula for n resistors in series:

Example:

Suppose we have three resistors in series with values ​​of 4Ω, 6Ω and 10Ω.

Special case: resistors of equal value

If all resistors have the same R value:

Where n is the number of resistors.

Example:

Suppose we have five resistors, each of 2Ω.

Resistors in parallel

When resistors are connected in parallel, calculating the total resistance is a little more complex. The total resistance is less than the resistance of each individual resistor.

General formula for n resistors in parallel:

To find R_tot​, you need to take the reciprocal of the sum of the reciprocals of the individual resistances.

Example:

Suppose we have three resistors in parallel with values ​​of 4Ω, 6Ω and 12Ω.

Let’s calculate the reciprocals:

Now let’s take the reciprocal of the sum:

Special case: resistors of equal value

If all resistors have the same R value:

So,

Where n is the number of resistors.

Example:

Suppose we have four resistors, each 8Ω.

Now let’s take the reciprocal of the sum:

These calculations allow you to determine the total resistance in different circuit configurations, helping you design circuits with the desired characteristics.

Summary

Resistors in series:

Special case for equal resistors:

Resistors in parallel:

Special case for equal resistors:

These calculations allow you to determine the total resistance in different circuit configurations, helping you design circuits with the desired characteristics.

The capacitors

Capacitors are fundamental electronic components used to store electrical energy in an electrostatic field. They find application in a wide range of electronic circuits, thanks to their ability to rapidly charge and discharge energy. Let’s see in detail what they are, how they work, what they are made of, the existing types, the units of measurement and their applications.

Structure and functioning

A capacitor is made up of two conductors separated by an insulator or dielectric. When a voltage is applied to conductors, they accumulate opposite charges, creating an electric field between them. The capacitance of the capacitor, which measures the amount of charge it can store per unit of applied voltage, is determined by the formula:

Where:

• C is the capacitance in farads (F)
• Q is the charge in coulombs (C)
• V is the voltage in volts (V)

Materials used

The main materials used in the construction of capacitors include:

• Conductors: typically made of aluminum, tantalum, or other metals.
• Dielectric: can be air, paper, plastic, ceramic, mica, tantalum oxide or various electrolytes.

The type of dielectric used greatly influences the properties of the capacitor, including its capacitance, working voltage, and its stability and reliability characteristics.

Types of capacitors

There are various types of capacitors, each with specific characteristics that make them suitable for different applications:

Electrolytic capacitors:

• They use an electrolyte as a dielectric.
• They have high capacitances (microfarads to millifarads).
• They are polarized, so they must be connected correctly.
• Used in power supplies and filter circuits.

Ceramic capacitors:

• They use ceramic as a dielectric.
• They have capacities from picofarads to microfarads.
• Not polarized.
• Used in high frequency applications and decoupling circuits.

Film capacitors:

• They use plastic films as a dielectric.
• They have capacities from picofarads to microfarads.
• Not polarized.
• Used in precision applications and for audio filtering.

Mica capacitors:

• They use mica as a dielectric.
• They have capacitance from picofarad to nanofarad.
• Not polarized.
• Used in high frequency applications and in resonance circuits.

Tantalum capacitors:

• They use tantalum oxide as a dielectric.
• They have capacities from nanofarads to microfarads.
• Polarized.
• Used in applications requiring high stability and reliability.

Unit of measurement

The capacitance of capacitors is measured in farads (F), which is a very large unit for most practical applications. Therefore, prefixes are used to express more common capabilities:

Uses of capacitors

Capacitors are extremely versatile and find use in many electronic applications, including:

1. Filtering: in power circuits, capacitors are used to smooth voltage variations and filter alternating current (AC) ripple. An electrolytic capacitor, for example, can smooth the voltage in a direct current (DC) power supply, ensuring a stable voltage.
2. Coupling and decoupling: in amplifier circuits, capacitors are used to couple amplification stages, allowing alternating (AC) signals to pass and blocking direct (DC) signals. This ensures that only the desired signals are amplified and propagated.
3. Timing circuits: capacitors, in combination with resistors, can form timing circuits (RCs). These circuits can generate time delays or specific oscillating frequencies, used in timers, oscillators, and clock circuits.
4. Oscillators and synthesizers: capacitors, in combination with inductors, form LC resonant circuits. These circuits are critical for generating signals at specific frequencies, such as those used in music synthesizers and radio broadcasts.
5. RF resonance and filtering: in radio frequency (RF) circuits, capacitors are used to select and filter specific frequencies. Mica and ceramic capacitors are particularly suitable for high-frequency applications due to their stability and precision.
6. Energy storage: supercapacity capacitors, also known as supercapacitors, can store large amounts of energy and release it quickly. These are used in applications such as photographic flashes, electric vehicles and backup power systems.
7. Smoothing: in power circuits, capacitors are used to smooth the output voltage by reducing ripple. This application is particularly important in AC/DC converters.
8. Voltage stabilization: capacitors are often used to stabilize the supply voltage in digital circuits, protecting against rapid voltage changes that can cause malfunctions.

Capacitors are key components in electronics, capable of storing and releasing energy quickly. Understanding their structure, the materials used, the types available, and their applications is critical to designing effective and reliable electronic circuits. Whether used to filter signals, couple amplification stages, or create timing circuits, capacitors remain irreplaceable in the world of electronics.

Calculation of total capacity

Series capacitors

When capacitors are connected in series, the total capacitance of the circuit is less than the capacitance of each individual capacitor. This happens because the total voltage divides between the capacitors, reducing the charge stored for a given voltage. The formula for calculating the total capacitance of series capacitors is:

Example:

Suppose we have three capacitors in series with capacities of 2µF, 4µF and 6µF.

Let’s calculate the reciprocals and add them:

Now let’s take the reciprocal of the sum:

Special case: capacitors of equal value

If all capacitors in series have the same capacitance C:

So,

Example:

Suppose we have four capacitors, each 8µF, in series.

Now let’s take the reciprocal:

Capacitors in parallel

When capacitors are connected in parallel, the total capacitance of the circuit is the sum of the individual capacitances. This is because the total stored charge is the sum of the charges stored by each capacitor for a given voltage.

General formula for n capacitors in parallel:

Example:

Suppose we have three capacitors in parallel with capacities of 2µF, 4µF and 6µF.

Special case: capacitors of equal value

If all capacitors in parallel have the same capacitance C:

Example:

Suppose we have four capacitors, each 8µF, in parallel.

Resistors and capacitors can be connected together to make more complex circuits. A very well known circuit is the RC circuit.

RC circuit: time and frequency domain analysis

An RC circuit consists of a resistor (R) and a capacitor (C) connected in series or parallel. It is a very common circuit in electronics, used for timing, filters and oscillators. In this section, we will examine the behavior of the RC circuit in both the time and frequency domains.

Time domain: process of charging and discharging the capacitor

Charging the capacitor

Initially we close the switch as in the figure below. When a capacitor is connected in series with a resistor to a voltage source, the capacitor charges over time.

The voltage V_C across the capacitor during charging is described by the formula:

Where:

• V₀​ is the supply voltage.
• R is the resistance in ohms.
• C is capacity in farads.
• t is the time in seconds.
• RC is the time constant of the circuit, denoted as τ.

The current I(t) in the circuit while charging the capacitor is:

Capacitor discharge

At this point, still keeping the switch closed, we “cancel” the generator, that is, we short-circuit the battery so as to have zero supply voltage, as in the following image:

When the charged capacitor is connected to a resistor without external power, it discharges over time. The voltage V_C across the capacitor during discharge is described by the formula:

The current I(t) in the circuit during the discharge of the capacitor is:

Frequency domain: Low Pass filter behavior

In the frequency domain, an RC circuit can function as a low-pass filter, allowing low frequencies to pass while attenuating high frequencies.

Capacitor impedance

The impedance Z_C of the capacitor as a function of the frequency f is:

Where ω=2πf is the angular pulsation.

Transfer function

The transfer function H(f) of an RC low-pass filter is:

Where f_c is the filter cutoff frequency, defined as:

At very low frequencies (f ≪ f_c), the gain is approximately 1, while at very high frequencies (f ≫ f_c), the gain decreases, attenuating the signals.

Magnitude and Phase

The magnitude ∣H(f)∣ and the phase ∠H(f) of the transfer function are given by:

At f = f_c, the magnitude of the gain is

of the maximum value, and the phase is -45°.

Practical example

Charge and discharge in the time domain

Suppose we have an RC circuit with R=1kΩ C=1μF. The time constant is:

If the supply voltage is V₀ = 5V:

The voltage across the capacitor during charging will be:

During the discharge, the voltage across the capacitor will be:

Low Pass Filter in the Frequency Domain

Using the following circuit with a variable frequency sine wave generator as input

and the values ​​of the resistor and capacitor respectively equal to R=1kΩ and C=1μF the cut-off frequency is:

while for f = f_c :

The RC circuit is a fundamental element in electronics, useful both in the time domain for capacitor charging and discharging operations, and in the frequency domain as a low-pass filter. Understanding these properties is essential for designing and analyzing effective electronic circuits. Now let’s look graphically at what we just saw.

Here are the graphs showing the behavior of the RC circuit in both the time and frequency domains:

1. Capacitor charge:
   • The graph shows how the voltage across the capacitor increases over time as it is charged. The voltage follows an exponentially increasing curve, asymptotically approaching the supply voltage.
2. Capacitor discharge:
   • The graph shows how the voltage across the capacitor decreases over time as it is discharged. The voltage follows a decreasing exponential curve, asymptotically approaching zero.
3. RC Low Pass Filter Frequency Response:
   • The graph shows the magnitude of the frequency response of the RC low-pass filter in decibels (dB). The filter allows low frequencies to pass through and attenuates high frequencies. The cutoff frequency f_c is the point where the magnitude drops 3 dB from the maximum value.

These graphs clearly illustrate the dynamic behavior of the RC circuit both during the charging and discharging processes in the time domain, and in the frequency response as a low-pass filter.

The inductors

Inductors are fundamental components in electronics that store energy in a magnetic field when a current flows through them. These devices are used in a variety of applications, including filtering, voltage transformation, and creating oscillators.

Structure and functioning

An inductor generally consists of a coil of conducting wire, often wrapped around a core of ferromagnetic material, such as iron or ferrite. When current flows through the coil, a magnetic field is generated around it. Energy is stored in this magnetic field and is released when the current is interrupted.

The fundamental property of inductors is inductance, which measures the inductor’s ability to store magnetic energy. Inductance L is measured in henries (H) and depends on the number of turns in the coil, the cross-sectional area of ​​the core, and the type of core material.

Materials used

Inductors can be made with different materials, each with specific characteristics:

• Iron: used in transformers and power reactors.
• Ferrite: used in high frequency applications, such as RF filters.
• Air: used in RF circuits and low power circuits.

Types of inductors

There are various types of inductors, each designed for specific applications:

1. Air core inductors:
   • They have no magnetic core, only coil of wire.
   • Used in RF applications and high frequency circuits.
   • Low inductance but high Q factor.
2. Iron core inductors:
   • They have an iron core which increases inductance.
   • Used in transformers and power reactors.
   • High inductance but can saturate at high currents.
3. Ferrite core inductors:
   • They have a ferrite core which offers a good combination of high inductance and high frequency.
   • Used in RF filters and switching power applications.
   • Excellent high frequency properties.
4. Variable inductors:
   • They have an adjustable core that allows you to vary the inductance.
   • Used in tuning circuits and oscillators.

Unit of measurement

Inductance is measured in henries (H), with prefixes used for more practical values:

• 1 henry (H)
• 1 millihenry (mH) = 10⁻³ henry
• 1 microhenry (µH) = 10⁻⁶ henry

Uses of inductors

Inductors are used in numerous applications thanks to their ability to store and release magnetic energy:

1. Filtering:
   • Used in low-pass, high-pass, band-pass and notch filters to eliminate interference and unwanted signals.
   • Commonly used in power supplies and audio circuits to smooth current ripple.
2. Transformers:
   • They combine two inductors on a common core to transform voltages and currents.
   • Essential for electricity distribution and power converters.
3. Oscillators:
   • Used in LC oscillator circuits to generate signals at specific frequencies.
   • They are used in radio transmitters and frequency synthesizers.
4. Load inductors:
   • Used as inductive loads in RF amplifiers and power circuits to improve stability and efficiency.
5. Reactance:
   • Used in reactance compensation circuits to balance inductive and capacitive loads.

Calculation of inductive reactance

Inductive reactance X_L​ is a measure of how much an inductor opposes alternating current (AC). It is given by the formula:

Where:

• X_L​ is the inductive reactance in ohms (Ω).
• f is the frequency of the signal in hertz (Hz).
• L is the inductance in henry (H).

Inductors are essential components in electronics, used for filtering, voltage transformation, oscillators, and much more. Understanding their structure, materials used, types available, and specific applications is critical to designing effective and reliable electronic circuits. Whether smoothing signals, transforming voltages or generating frequencies, inductors remain indispensable in the world of electronics.

Calculation of inductors in series and parallel

Inductors can be connected in series or parallel, and their overall inductances can be calculated similarly to resistors. Let’s see how the total inductance is calculated for both configurations.

Inductors in series

When inductors are connected in series, the current flowing through them is the same for each inductor, while the total voltage across the series is the sum of the voltages across the individual inductors. The total inductance L_tot is the sum of the individual inductances.

General formula for n inductors in series:

Example:

Suppose we have three inductors in series with inductances of 2H, 3H and 4H.

Special case: inductors of equal value

If all inductors have the same inductance L:

Where n is the number of inductors.

Example:

Suppose we have four inductors, each of 5H.

Inductors in parallel

When inductors are connected in parallel, the voltage across each inductor is the same, while the total current is the sum of the currents in the individual inductors. The total inductance L_tot​ can be found using the sum of the reciprocals of the individual inductances.

General Formula for n Inductors in Parallel:

To find L_tot​, you need to take the reciprocal of the sum of the reciprocals of the inductances.

Example:

Suppose we have three inductors in parallel with inductances of 4H, 6H and 12H.

Let’s calculate the reciprocals:

Now let’s take the reciprocal of the sum:

Special case: inductors of equal value

If all inductors in parallel have the same inductance L:

So,

Where n is the number of inductors.

Example:

Suppose we have five inductors, each 10H, in parallel.

Now let’s take the reciprocal:

Summary

Series inductors:

Special case for equal inductors:

Inductors in parallel:

Special case for equal inductors:

These calculations allow you to determine the total inductance in different circuit configurations, helping you design circuits with the desired characteristics.

Study of the behavior of an RLC circuit in the time domain

An RLC circuit consists of a resistor (R), an inductor (L) and a capacitor (C) which can be connected in series or parallel. In this case we consider them connected in series. When the circuit is connected to a battery and the switch is closed, a transient response characterized by damped oscillations is observed. This type of circuit is crucial for understanding phenomena such as resonance and oscillation in electrical circuits.

Differential equation of the RLC circuit

The differential equation describing the behavior of a series RLC circuit is:

Where:

• L is the inductance in henry (H).
• R is the resistance in ohms (Ω).
• C is the capacitance in farads (F).
• i(t) is the current in the circuit as a function of time.
• V₀​ is the supply voltage in volts (V).

Solution of the differential equation

The solution of the differential equation depends on the values ​​of R, L and C. In particular, three cases can be distinguished based on the damping factor ζ:

1. Overdamping (ζ>1) leads to a response without oscillations, with a slow return to equilibrium.
2. Critical Damping (ζ=1) represents the limiting case in which the circuit returns to equilibrium in the shortest possible time without oscillating.
3. Underdamping (ζ<1) involves oscillations that dampen over time.

In the case of a pure RLC circuit (where there are no active elements such as, for example, a transistor) the oscillations dampen over time due to the losses introduced by the resistor.

The current in the circuit for the underdamped case is:

Where:

the damping factor is:

the damped oscillation frequency is:

the natural frequency of the circuit is:

the initial amplitude of the current is:

I₀

Voltage at the ends of the resistance

The voltage across the resistor V_R(t) is given by:

This voltage shows an initial overshoot and oscillates, dampening over time until it reaches the steady-state value.

Time domain behavior graph

Now, let’s draw the graph of the voltage across the resistor V_R(t) for an underdamped RLC circuit.

Circuit parameters:

• R = 1 Ω
• L = 1 H
• C = 100 μF
• V₀ = 10 V

Calculated constants:

The following image shows the voltage trend across the resistor:

The graph highlights how the voltage across the resistor grows rapidly, reaches a peak (overshoot) and then oscillates, dampening over time until it stabilizes. This is a typical transient response of an underdamped RLC circuit.

In the series RLC circuit, the voltage across the resistor stabilizes at 0V at steady state because the capacitor charges to the supply voltage and, once fully charged, prevents the flow of current through the circuit. This means that there will be no current flowing through the resistor at steady state, and therefore the voltage across the resistor will be zero. Let’s see how to explain this concept in detail.

Explaining behavior in the time domain

When a series RLC circuit is connected to a battery via a switch, initially, as the switch is closed, a transient response is observed. During this transient period, if there is the condition ζ<1, the voltage across the resistor V_R(t) exhibits damped oscillating behavior, which is typical of an underdamped RLC circuit.

Phases of the transient response:

1. Start of charging:
   • When the switch is closed, the capacitor is initially discharged and the circuit behaves as if the capacitor were a short circuit.
   • The current begins to flow rapidly, causing the voltage across the resistor to rapidly increase.
2. Overshoot:
   • Due to the presence of the inductor, the magnetic energy stored in the inductor’s magnetic field causes current to continue to flow beyond the initial equilibrium point, causing an overshoot in the voltage across the resistor.
3. Damped oscillations:
   • The circuit oscillates due to the fact that energy is exchanged between the magnetic field of the inductor and the electric field of the capacitor.
   • The oscillations are gradually dampened due to the resistor dissipating the energy in the form of heat.
4. Stationary regime:
   • Eventually, the capacitor charges to the supply voltage and reaches a steady state where there is no more current flowing in the circuit.
   • At steady state, the current is zero and the voltage across the resistor is zero because the capacitor prevents the passage of current.

Behavior of an RLC circuit in the frequency domain

In the frequency domain, a series RLC circuit can be analyzed as a bandpass filter. Instead of the battery we will have a variable frequency sinusoidal generator at the input. This filter allows frequencies close to the resonance frequency to pass through and attenuates frequencies outside this band. Let’s see how this circuit works and how it can be described mathematically.

Transfer function

The transfer function H(jω) of a series RLC circuit is given by the relationship between the output voltage and the input voltage of the circuit. Considering V_in the input voltage and V_out the voltage across the resistor, we have, referring to the circuit in the figure below:

Where:

• ω is the angular pulsation, with ω=2πf, where f is the frequency in hertz (Hz).
• R is the resistance in ohms (Ω).
• L is the inductance in henry (H).
• C is the capacitance in farads (F).

The transfer function describes how the amplitude and phase of the signal are changed through the circuit.

Resonance frequency

The resonant frequency f₀ of the RLC circuit is the frequency at which the impedance of the circuit is purely resistive and the energy stored in the inductor and capacitor is maximum. It is given by:

At the resonant frequency, the inductance and capacitance cancel each other out, and the transfer function reaches its maximum.

Bandwidth

The passband of the filter, i.e. the frequency range for which the signal passes through the circuit without being significantly attenuated, is determined by the points at which the frequency response is

of the maximum value. The bandwidth Δω is:

Frequency response

The frequency response H(jω) can be analyzed in terms of magnitude and phase. The magnitude of the transfer function is:

And the phase is:

Interpretation of the graph

The frequency response graph shows:

1. Resonance frequency (f₀​):
   • At the resonant frequency f₀, the frequency response reaches its maximum (peak). This is the point where the circuit impedance is at its lowest and the signal passes with the least attenuation.
2. Bandwidth:
   • Bandwidth is the range of frequencies around f₀ where the frequency response is significant. The bandwidth is determined by the resistance and inductance of the circuit.
3. Out-of-band attenuation:
   • Outside the passband, the frequency response decreases rapidly, attenuating signals that are far from the resonant frequency.

The behavior of an RLC circuit in the frequency domain is critical to many electronic applications, such as the design of filters and resonators. The circuit acts as a band-pass filter, allowing frequencies near the resonant frequency to pass through and attenuating frequencies far from it. This behavior is described by the transfer function, which can be analyzed in terms of magnitude and phase to understand how the circuit modifies the input signals.

The diodes

Diodes are fundamental electronic components that allow current to flow in only one direction. They play a crucial role in a wide range of electronic applications, from alternating current (AC) rectification to circuit protection.

What are diodes

A diode is a two-terminal device that allows current to flow primarily in one direction, while blocking it in the other. This property is known as unidirectional conduction. The schematic symbol of a diode shows an arrow indicating the direction of the allowable current.

What are diodes for?

Diodes are used in multiple applications, including:

1. Rectification: conversion of alternating current (AC) to direct current (DC) in power circuits.
2. Protection: protection of circuits from overvoltages and reverse polarity.
3. Voltage regulation: voltage stabilization in electronic circuits.
4. Detection and mixing: use in RF circuits for detection and mixing of signals.
5. Light emitting: light emitting diodes (LEDs) are used in displays, lighting and status indication.

Structure and materials

Diodes consist of a p-n junction, an interface between two oppositely doped semiconductor materials (p-type and n-type). When a positive voltage is applied to the p-type terminal compared to the n-type terminal (forward bias), the diode conducts current. Otherwise, when the voltage is reversed (reverse biased), the diode blocks the current.

Materials used

• Silicon: most modern diodes are made of silicon, which offers good switching characteristics and high threshold voltages (around 0.6V – 0.7V).
• Germanium: used in early semiconductor diodes, germanium diodes have a low threshold voltage (about 0.3V) but are less common today due to their inferior characteristics compared to silicon.
• Gallium Arsenide: used in high-frequency diodes and LEDs, it offers excellent high-speed switching properties.

Vacuum diodes

Before the invention of semiconductor diodes, vacuum diodes were commonly used. These devices consist of a heated cathode that emits electrons and an anode that collects these electrons in an air-free (vacuum) environment. Vacuum diodes were used in early radios and televisions to rectify the current.

Types of diodes and their uses

1. PN junction diodes:
   • the most common, used for rectification and circuit protection.
2. Zener diodes:
   • designed to operate in reverse bias beyond breakdown voltage, used for voltage regulation.
3. LED diodes:
   • they emit light when directly polarized, used in displays, status indicators and lighting.
4. Schottky diodes:
   • they have a low forward voltage drop and are used in high-speed applications.
5. Photovoltaic Diodes (solar diodes):
   • they convert sunlight into electricity, used in solar panels.
6. Tunnel Diodes:
   • used in high frequency and microwave applications due to their fast switching characteristics.
7. Varicap diodes:
   • used as voltage-controlled variable capacitors in tuning circuits.

Diodes are essential components in modern electronics, used to control the direction of current flow and for a wide range of other applications. From early vacuum diodes to modern silicon diodes and LEDs, the evolution of diodes has had a significant impact on the development of electronic technology. With an understanding of their different types and applications, diodes continue to be critical to the design and operation of electronic circuits.

Analysis of a particular diode: the LED

Light-emitting diodes (LEDs) are a particular class of diodes that emit light when an electric current passes through them. They have become extremely popular for their energy efficiency, long life and versatility in lighting and display applications.

What is an LED

An LED is a semiconductor device that emits light when a current flows through it in forward bias. The operating principle of LEDs is based on electroluminescence, a phenomenon in which a material emits light in response to an electric current.

Structure and materials

LEDs consist of a p-n junction formed from compound semiconductor materials, such as gallium arsenide (GaAs), gallium phosphide (GaP), and gallium nitrate (GaN). These materials are chosen based on the wavelength of light they emit, determining the color of the LED.

• p-n junction: similar to other diodes, the p-n junction of the LED is made of oppositely doped semiconductor materials. When a current passes through the junction, the electrons and holes recombine, emitting photons.
• Substrate material: often the LED is built on a sapphire or silicon carbide substrate to provide mechanical stability and improve efficiency.

LED operation

When an LED is forward biased (the anode is positive relative to the cathode), the electrons in the n-type material move towards the p-type region and the holes in the p-type material move towards the n-type region. When electrons recombine with holes in the junction region, they release energy in the form of photons, emitting light.

The wavelength (and therefore the color) of the light emitted depends on the semiconductor material used:

• GaAs: emits infrared light.
• GaAsP: emits red or orange light.
• GaP: emits green light.
• GaN: emits blue or UV light.

Advantages of LEDs

1. Energy efficient: LEDs use significantly less energy than incandescent bulbs and fluorescent tubes, reducing energy costs.
2. Long life: LEDs have a very long operating life, often exceeding 50,000 hours.
3. Durability and reliability: LEDs are rugged and resistant to shock and vibration, making them ideal for applications in harsh environments.
4. Small size: LEDs come in very small sizes, allowing for integration into compact devices.
5. Quick On: LEDs turn on instantly with no warm-up time.

LED applications

1. Lighting: LEDs are widely used in light bulbs, spotlights, street lighting and architectural lighting for their energy efficiency and long life.
2. Displays and signs: used in LED screens, illuminated signs, traffic lights and billboards.
3. Status indicators: used in consumer electronics, industrial equipment, and automobiles to indicate operating status.
4. Backlight: used in LCD displays of televisions, monitors, smartphones and tablets.
5. Automotive lighting: used in vehicle headlights, tail lights and daytime running lights.
6. Medical applications: used in medical light therapy devices and surgical instruments.

Evolution of LEDs

1. Infrared diodes: early LEDs emitted infrared light and were primarily used in remote controls.
2. Red and green LEDs: developed in the 1960s, they were used in displays and indicators.
3. Blue LEDs: the development of blue LEDs in the 1990s paved the way for the creation of white LEDs by combining them with phosphors or mixing colors (RGB).
4. White LEDs: white LEDs are now used for general lighting, offering an efficient alternative to traditional bulbs.

Technical considerations

• Threshold voltage: LEDs require a specific threshold voltage to begin conducting. For example, red LEDs require approximately 1.8V, while blue and white LEDs require approximately 3.0V.
• Operating current: the operating current must be controlled using resistors or driving circuits to avoid overheating and ensure long life of the LED.
• Heat dissipation: high-power LEDs generate heat that must be dissipated using heat sinks to maintain device efficiency and life.

LEDs represent one of the most significant innovations in modern electronics. With their energy efficiency, long life and versatility, LEDs have revolutionized lighting and display technologies. Understanding how they work, the materials used and their applications is essential to make the most of the potential of these constantly evolving devices.

LEDs are often used in our projects with Arduino, ESP32 and other boards. They are generally activated by a GPIO of the microcontroller used which powers them (turns on) or not (turns off) with a voltage of 5V or 3.3V depending on the microcontroller. LEDs generally cannot withstand high power currents, in fact they risk burning out immediately if the necessary precautions are not taken. One method to limit the current is to place a limiting resistor between the GPIO and the LED to avoid burning it (and burning the digital output to which it is connected).

Let’s see a calculation example assuming that the digital outputs of the microcontroller we are using are at 3.3V.

The LED has two terminals (called anode and cathode) and, like all diodes, it is a component that has its own polarity: it passes the current when it is forward polarized (i.e. the voltage at the anode is greater than that at the cathode) and it blocks current when it is reverse polarized (i.e. the anode voltage is lower than the cathode voltage). The voltage between the anode and cathode, which we will indicate with Vd, varies according to the color of the light emitted. In particular we have that:

• V_d = 1.8 V for red LEDs
• V_d = 1.9 V for yellow LEDs
• V_d = 2 V for green LEDs
• V_d = 2 V for orange LEDs
• V_d = 3 V for blue LEDs
• V_d = 3 V for white LEDs

How do we identify the anode and cathode of the LED? We do this by looking at its terminals. The longest corresponds to the anode. Also, the LED body has a flattening at one point on the edge indicating that the nearby terminal is the cathode.

So if an LED doesn’t light up it’s possible that it’s wired upside down. In this case, to make it work, simply reverse the connections.

How do you calculate the resistance to connect to the LED?

As we have already said, the resistor between the generic GPIO and the LED serves to limit the current flowing through the LED. But how can we calculate its resistance value? Ohm’s Law comes to our aid which says that the potential difference across a resistor (i.e. the voltage measured at the ends of the resistor) is proportional to the current I flowing through it and the constant of proportionality is precisely the resistance value of the resistor R:

V2 - V1 = RI

Please note: for the sake of precision it must be pointed out that while the resistor is the physical component (the actual object), the resistance is its value. So it is improper (even if it happens frequently) to call the resistor with the term resistance.

We can see Ohm’s Law on a simple circuit consisting of a voltage source (the circle on the left) and a resistor:

The voltage (or potential difference) V2 – V1 impressed by the voltage source on the resistor is equal to the product of R by I.

Now let’s see a slightly more complex scheme where the usual voltage generator, the resistor and a red LED are present:

In our case the Vg represents the voltage present at the digital output of our board when it is HIGH and is therefore equal to 3.3V.

Vd is the voltage across the diode (between anode and cathode) when it is forward biased (ie when it is carrying current). Having chosen a red LED, we know from the previous table that Vd = 1.8V.

We need to determine the R-value of the resistor. We still have one unknown: the value of the current I which must flow in the circuit when the pin is in the HIGH state.

Please note: when the digital pin is in the LOW state its voltage (ie Vg) is zero, it follows that also the current I in the circuit is zero.

LEDs generally cannot withstand currents greater than 20mA, so we impose a maximum current of 15mA to be on the safe side.

By Kirchhoff’s voltage law we have that:

Vg - Vr - Vd = 0

From which we derive that:

Vr = Vg - Vd 

Passing to the real values, we have that:

Vr = 3.3V - 1.8V

It follows that:

Vr = 1.5V

But, by Ohm’s Law, we have that:

Vr = RI

from which:

R = Vr / I

Substituting the real values:

R = 1.5V / 0.015A

The result is a value of R equal to 100Ω.

Let’s now look at another very important application of the diode.

The diode as a rectifier in power supplies

The diode is commonly used as a rectifier in power supplies to convert alternating voltage (AC) to direct voltage (DC). A basic rectification circuit consists of an AC voltage source (for example a transformer that lowers the 230V AC mains voltage to much lower values), a diode and a resistive load connected in series.

Circuit composition:

• Alternating voltage (AC) generator: generates an alternating sinusoidal voltage, for example, with a peak of 12V. It may be the secondary winding of a voltage reducing transformer.
• Diode: allows the passage of current only during the positive half-waves of the AC voltage.
• Resistive load: a resistor that represents the load on which we want to obtain the rectified direct voltage.

Circuit operation

1. Positive half-wave:
   • During the positive half-wave of the AC voltage, the anode of the diode is positive relative to the cathode.
   • The diode is forward biased and conducts current.
   • The current passes through the diode and the resistive load, generating a voltage across the resistor.
2. Negative half-wave:
   • During the negative half-wave of the AC voltage, the anode of the diode is negative relative to the cathode.
   • The diode is reverse biased and does not conduct current.
   • Current does not pass through the diode, so there is no voltage across the resistor.

The result is a voltage across the resistive load that consists only of the positive half-waves of the original AC voltage.

Circuit behavior graph

The graph shows the input voltage (AC voltage) and the voltage across the load (rectified voltage) over time.

Circuit parameters:

• AC peak voltage: 12V
• AC Frequency: 50Hz
• Resistive load: 1kΩ (as an example)

Description of the graphs

1. AC Input Voltage :
   • The top graph shows the input AC voltage with a peak of 12V and a frequency of 50Hz.
   • The voltage varies sinusoidally from +12V to -12V.
2. Rectified Voltage Across Load:
   • The lower graph shows the voltage across the load after rectification.
   • During the positive half-waves of the AC voltage, the diode is forward biased and conducting, so the voltage across the load follows the positive half-wave.
   • During negative half-waves, the diode is reverse biased and does not conduct, so the voltage across the load is zero.

The diode used as a rectifier in power circuits allows a rectified voltage to be obtained from an alternating voltage. This process is essential for many electronic applications that require a stable DC voltage. The graph clearly shows how the diode blocks the negative half-waves and lets only the positive half-waves pass, thus rectifying the voltage.

Obviously a pulsating unidirectional voltage like the one obtained is not yet suitable for powering the load. We must filter it in order to make it continuous (and therefore no longer pulsating). To do this we add a filter capacitor in parallel to the load.

By adding a filter capacitor in parallel to the load, we improve the quality of the rectified voltage, reducing ripples. The circuit now consists of:

• A 12V peak alternating voltage (AC) generator.
• A rectifier diode.
• A resistive load.
• A filter capacitor in parallel with the load.

Circuit operation

1. Positive half-wave:
   • During the positive half-wave, the diode is forward biased and conducts current.
   • The capacitor charges rapidly to the peak of the input voltage.
2. Negative half-wave:
   • During the negative half-wave, the diode is reverse biased and does not conduct.
   • The capacitor, charged to the peak voltage, supplies current to the resistive load, keeping the voltage across it relatively constant until the next positive half-wave.

Ranges in which the diode conducts

The diode conducts primarily during positive half-waves, particularly when the input voltage exceeds the voltage on the capacitor, charging the capacitor again to the peak of the input voltage.

Circuit behavior graph

The graph shows the voltage across the load with and without the filter capacitor to compare the effectiveness of the filtering.

Circuit parameters:

• AC peak voltage: 12V
• AC Frequency: 50Hz
• Resistive load: 1kΩ
• Capacitance Capacitance: 100μF (as example)

Here is the graph showing the behavior of the circuit with a rectifier diode and a filter capacitor in parallel to the load, extended over several periods:

1. Rectified Voltage Across Load Without Filter:
   • The upper graph shows the voltage across the load without the filter capacitor. The voltage follows the positive half-waves of the AC voltage, with intervals where the voltage is zero during the negative half-waves.
2. Filtered Voltage Across Load with Capacitor:
   • The bottom graph shows the voltage across the load with the filter capacitor. The capacitor significantly reduces ripples, maintaining a more constant voltage across the load. When the diode is cut off, the capacitor slowly discharges through the load, providing current and maintaining the voltage until the next positive half-wave.
   • Therefore, unlike the case without a capacitor, the diode no longer conducts during the entire duration of the positive half-wave but only in the short time interval between the instant in which the voltage applied to the diode exceeds that at which the capacitor was charged and the instant the voltage reaches its peak (as represented by the blue graph). At all other times the diode is reverse biased and does not conduct. In this time interval the capacitor discharges onto the load until the next moment in which the diode resumes conducting and charging the capacitor.

By adding a filter capacitor in parallel to the load in a rectification circuit, we obtain a more stable DC voltage and reduce ripple. This process significantly improves the quality of the rectified voltage, making it more suitable for powering sensitive electronic devices.

By increasing the value of the capacitor it is possible to reduce the residual ripple of the voltage (the so-called ripple).

The transistor

We arrive at one of the most important components of modern electronics: the transistor.

Transistor is a semiconductor electronic component that can amplify or switch electrical signals. Invented in 1947, it is one of the fundamental components of modern electronics. Transistors are essential for building analog and digital circuits, from simple amplifiers to complex microprocessors.

What is the transistor for?

Transistors have two main functions:

1. Amplification: they can increase the strength of a weak signal.
2. Switching: they can function as electronic switches, turning circuits on and off.

Types of transistors

There are different types of transistors, each with specific characteristics. The main types of transistors include:

1. Bipolar Junction Transistor (BJT):
   • Composed of three layers of n- and p-type semiconductor material.
   • Available in NPN and PNP configurations.
2. Field Effect Transistor (FET):
   • Includes MOSFET (Metal-Oxide-Semiconductor FET) and JFET (Junction FET).
   • It uses an electric field to control the flow of current.

Although there are various types of transistors, we will focus on bipolar junction transistors (BJTs) in this description.

Bipolar Junction Transistor (BJT)

BJTs are made up of three layers of semiconductor material: emitter (E), base (B), and collector (C). BJTs can be of the NPN or PNP type, depending on the type of semiconductor used.

• NPN: the current flow is from the emitter to the collector through the base.
• PNP: the current flow is from the collector to the emitter through the base.

Operation of the BJT

The operation of a BJT is based on the polarization of the p-n junctions:

• Forward bias: the base-emitter junction is forward biased, allowing current to flow.
• Reverse bias: the base-collector junction is reverse biased, controlling the main current flow through the transistor.

The current flowing between collector and emitter is controlled by the base current. A small change in base current can cause a large change in collector current, thus allowing signal amplification.

Applications of the transistor

Analog electronics

1. Amplifier:
   • Transistors are used in amplifiers to increase the power of weak signals.
   • Common configurations include common-emitter, common-collector, and common-base amplifier.
2. Oscillator:
   • Transistors can be used to create oscillators, which generate signals at specific frequencies.
   • Examples include the relaxation oscillator and the Wien bridge oscillator.
3. Voltage regulators:
   • Used in voltage regulation circuits to maintain a constant output voltage.

Digital electronics

1. Switch:
   • Transistors can function as electronic switches, controlling the flow of current in a circuit.
   • In switching mode, the transistor is either fully on (saturation) or fully off (cutoff).
2. Logic gates:
   • Transistors are key components in logic gates, which are the fundamental building blocks of digital circuits.
   • NOT (Inverter) port: uses a single transistor to invert the input signal.
   • AND Gate: uses two or more transistors in series to produce a high output only when all inputs are high.
   • OR Gate: uses two or more transistors in parallel to produce a high output when at least one input is high.

Example of using the transistor as an amplifier

Common emitter amplifier

A common-emitter amplifier is a very common amplification configuration that uses a BJT transistor.

• Input: the signal to be amplified is applied to the base of the transistor.
• Output: the amplified signal is taken from the collector.
• Load resistor: connected to the collector, determines the gain of the circuit.

Example of using the transistor as a switch

Switching circuit

A transistor can be used to control a load such as a relay (in particular its winding which is nothing more than an inductor).

• Input: the control signal is applied to the base of the transistor.
• Output: the relay winding is connected between the collector of the transistor and the power line.
• Operation: when the control signal is high, the transistor conducts and causes a current to conduct in the relay winding causing it to trip. When the control signal is low, the transistor is turned off, no more current flows in the relay winding which returns to its rest position.

Transistors are versatile and indispensable components in modern electronics. From their use as amplifiers and oscillators in analog circuits, to their crucial role as switches and in logic gates in digital circuits, transistors have revolutionized the world of electronics. Understanding how they work and their applications is essential for anyone working in the electronics field.

Let’s now try to analyze in more depth what is the most important use of the transistor in analog electronics: the signal amplifier.

Design of a common-emitter amplifier stage

Goals:

• Supply voltage: 12V
• Gain: at least 10
• Passband at -3dB: 20Hz to 20kHz
• Transistor: BC238
• Input impedance of a few tens of kΩ

BC238 Transistor Specifications:

• β (hFE): Typically 200

Steps for the project

Selection of the working point (Q-point):

• V_CC = 12V
• IC ≈ 1mA (collector current)

Calculation of base resistances (R₁ and R₂):

• The base voltage V_B​ must be such as to guarantee correct polarization of the transistor. Typically, V_B​ = V_E + 0.7V, where V_E is the voltage at the emitter and 0.7V is the voltage drop at the Base – Emitter junction when forward biased (as in the case of the silicon diode).
• V_E ≈ 1V, so V_B​ = 1V + 0.7V (a common choice is to have V_E between 1V and 2V)

Calculation of the emitter resistance (R_E):

• R_E =V_E / I_E ≈ 1V / 1mA = 1kΩ
• Note: I_E ≈ I_C for large values ​​of β.

Calculation of collector resistance (R_C):

• The voltage drop across R_C must be such that it leaves sufficient voltage on the collector. Typically, to stay in the linear zone, the collector is polarized so that it has a voltage equal to half the supply voltage.
• V_CE ≈ 6V (for good linearity), so the voltage drop across R_C is V_RC = V_CC − V_CE = 12V − 6V =6V.
• R_C = V_RC / I_C ≈ 6V / 1mA = 6kΩ.

Calculation of base voltage divider resistances (R₁ and R₂):

• The current through the divider I_R1R2​ must be at least 10 times the base current I_B​.
• I_B = I_C / β ≈ 1mA / 200= 5uA.
• I_R1R2​ ≈ 10 × I_B = 50uA.
• R₂ = V_B / I_R1R2​ = 1.7V / 50uA = 34kΩ.
• R₁ is determined by the V_CC voltage and the voltage drop across R₂​: R₁ = (V_CC − V_B) /I_R1R2​ = (12V − 1.7V) / 50uA ≈ 204kΩ.

The rule of thumb of making the current through the base voltage divider at least 10 times the base current I_B is to ensure that the bias voltage V_B​ is stable and not significantly affected by the base current itself. This practice helps maintain thermal stability and reduce variations in the operating point due to variations in β of the transistor.

Input impedance:

• Z_in ≈ R₁ ∥ R₂ ∥ (β R_E).
• Z_in ≈ 204kΩ ∥ 34kΩ ∥ (200×1kΩ) ≈30kΩ.

Coupling and bypass capacitors (C_in, C_E, C_out):

• the lower cutoff frequency (f_L​) is determined by these capacitors.
• in general f_L​ = 1 / (2πRC) where R is the impedance seen by the capacitor C.
• C_in: determines the input bandwidth. If Z_in ≈ 30kΩ: C_in = 1 / (2π × 20Hz × 30kΩ) ≈ 265nF.
• C_E: bypass the emitter resistor to increase the gain. C_E = 1 / (2π ×20Hz × R_E) ≈ 8uF.
• C_out​: determines the output bandwidth. Assuming Z_out ≈ R_C ∥ R_L​: C_out​ = 1 / (2π × 20Hz × 6kΩ) ≈ 1.3uF where R_L represents the possible load of the transistor (which can be a load or the input of a subsequent stage) and can be modeled with a resistor with a value equal to R_L connected between the free end of the C_out​ and the ground.

In the design of a common-emitter amplifier, in addition to the lower cut-off frequency determined by the coupling capacitors and the bypass capacitor on the emitter, it is also essential to consider the upper cut-off frequency. This depends on the internal capacitances of the transistor, which influence the frequency response of the circuit.

Internal capacitances of the transistor

1. Base-Collector Capacity (C_bc):
   • It is the intrinsic capacitance between the base and collector of the transistor.
   • This capacitance is particularly important because, through the Miller effect, it is “amplified” by the amplifier’s gain, significantly affecting the upper cut-off frequency.
2. Base-Emitter Capacity (C_be​):
   • It is the capacitance between the base and the emitter of the transistor.
   • Although generally smaller than C_bc​, it contributes to the reduction of the upper bandwidth.

Miller effect

The Miller effect amplifies the C_bc capacitance in a common-emitter amplifier circuit. The capacitance seen between the base and the collector is actually increased by a factor related to the gain of the circuit.

C_Miller = C_bc (1 + A_v) where A_v is the voltage gain of the amplifier stage.

This additional capacitance, C_Miller, has a significant effect on the upper cutoff frequency by reducing it, thus reducing the bandwidth.

Upper Cutoff Frequency (f_H​)

The upper cutoff frequency can be approximated by considering the feedback network impedance and internal capacitances. The general formula for the upper cutoff frequency is:

Where R_in is the input impedance seen from the base of the transistor.

The upper cutoff frequency of a common-emitter amplifier is strongly influenced by the internal capacitances of the transistor, particularly C_BC, and by the Miller effect which amplifies this capacitance. To ensure that the amplifier operates correctly in the desired frequency band, it is essential to consider these capacitances during the design process. Although the external capacitors determine the lower cutoff frequency, the internal capacitances of the transistor and the Miller effect play a crucial role in defining the upper cutoff frequency.

Considerations on approximations and rules of thumb used in the design of a common-emitter amplifier

The common-emitter amplifier design presented above is based on a series of approximations and rules of thumb that arise from engineering experience. These simplifications allow you to create an effective and practical project without having to deal with complex analytical calculations. However, it is important to recognize the limitations and nature of these approximations.

Approximations used

1. Working point (Q-point):
   • The operating point setting is based on conventional choices such as emitter voltage V_E ≈ 1V and collector current I_C = 1mA. These choices are made to ensure stable bias and good linearity, but are approximations that could be refined in more detailed analysis.
2. Base voltage divider:
   • The rule of thumb of making the current through the base voltage divider at least 10 times the base current I_B is an approximation that aims to ensure the stability of the bias voltage V_B​. This choice prevents variations in β of the transistor from significantly influencing the operating point.
3. Coupling and bypass capacitors:
   • Capacitor values ​​are calculated using time constants to obtain the desired lower cutoff frequencies. Here too, approximations are used to simplify the calculations.
4. Gain and bandwidth:
   • The gain is approximated by mainly considering the collector and emitter resistances. The upper cutoff frequency is considered through a qualitative understanding of the internal capacitances of the transistor and the Miller effect. In general, the higher the gain of the single stage, the narrower its bandwidth. For this reason, when it is desired to have a high overall gain with a fairly wide bandwidth, multiple stages are used in cascade (multistage amplifiers), considering that the overall gain of the amplifier (multistage) will be given by the product of the gains of the individual stages .

Rules of thumb

1. Base voltage divider:
   • Use a base voltage divider current 10 times greater than the base current to ensure good bias.
2. Voltage drop on the emitter:
   • Maintain a voltage drop of approximately 1V across the emitter to ensure good thermal stability.
3. Capacitor sizing:
   • Use RC time constants to determine the values ​​of the coupling and bypass capacitors, thus ensuring the desired lower cutoff frequencies.

Limits of approximations

1. Operating point accuracy:
   • Approximations can lead to a slight inaccuracy in the actual operating point of the transistor, which may not be exactly what is desired. This can affect the linearity and dynamic behavior of the circuit.
2. Parasitic effects:
   • Parasitic capacitances, parasitic inductances, and other nonlinear effects are not taken into account in simplistic approximations, but can have a significant impact in high-frequency or high-precision applications.
3. Variability of components:
   • Variability in component values ​​(e.g., resistor and capacitor tolerances) and variations in transistor parameters (β, V_BE, etc.) can lead to deviations from expected behavior.

Importance of approximations

Despite these limitations, approximations and rules of thumb are powerful and useful tools in practical engineering. They allow you to:

• Reduce the complexity of calculations.
• Speed ​​up the design process.
• Provide solutions accurate enough for many real-world applications.

The presented common-emitter amplifier design is based on a combination of approximations and rules of thumb, which allow obtaining an effective and functional design in a simplified way. Although exact calculations and precise determination of the transfer function require more in-depth and detailed analysis, engineering approximations provide a quick and practical method to address most design needs. These simplifications are generally acceptable and reliable for many practical applications, making them valuable tools for engineers.

Use of the transistor in digital circuits

Transistors are also crucial in digital circuits, where they function primarily as switches. Let’s see how to use transistors to implement NOT, AND and OR logic gates with up to 2 inputs.

NOT gate (inverter)

An inverter (NOT gate) is a circuit that inverts the logic level of the input signal. It uses a transistor in switching configuration.

Description of operation:

• High input (X = V_cc): the transistor is forward biased, conducting and saturating, so the output is low (0V).
• Low input (X = 0V): the transistor is off, it does not conduct, so the output V_out​ is high (+Vcc).

AND gate

A two-input AND gate produces a high output only if both inputs are high. It uses two NPN transistors in series.

Description of operation:

• Both input high(X = V_cc, Y = V_cc): both transistors conduct current through the R on the emitter. Consequently, the voltage at its terminals is non-zero (equal to RI) and therefore the output is high.
• One or both inputs low (X = 0V o Y = 0V): at least one of the transistors does not conduct, therefore no current flows through the resistor and consequently the voltage across it is low (logic level 0).

OR gate

A two-input OR gate produces a high output if at least one input is high. It uses two NPN transistors in parallel.

Description of operation:

At least one of the input high (X = V_cc o Y = V_cc): the corresponding transistor is forward biased and conducts, causing current to flow from Vcc ​ to GND through the transistor and the resistor on the emitter. Therefore there will be a positive voltage (approximately equal to Vcc) on the output and therefore a high logic level at the output.

Both inputs low (X = 0V e Y = 0V): none of the transistors are forward biased, so they don’t conduct. No current flows in the resistor connected to the emitters, consequently the voltage across it is zero and the output is low (0V).

Conclusions

We took a journey through the fundamental components of electronics, exploring resistors, capacitors, inductors, diodes, LEDs and transistors. Each component has its own peculiarities and applications, both in the world of analogue and digital electronics.

We started with resistors, analyzing their properties and applications, such as sizing in circuits and use in current and voltage control. Capacitors were explored in depth, with an analysis of their role in energy storage and release, and their applications in filters and timing circuits. Inductors have been described as devices for storing magnetic energy, used in filters and transformers.

The journey continued with diodes, describing their crucial role in current rectification and protection applications. We have delved into the importance of LEDs in the field of lighting and display, analyzing their energy efficiency and long life.

The transistor, one of the most revolutionary inventions of the 20th century, has been examined in both analog and digital applications. We’ve seen how transistors can amplify weak signals and function as switches in logic circuits. Through practical examples, we have implemented amplifier circuits, logic gates such as NOT, AND and OR, demonstrating the versatility and importance of transistors in modern electronics.

A small step into the sea of ​​electronics

This article represents a small drop in the vast sea of ​​electronics. We have just scratched the surface of a vast and ever-evolving field. Each topic covered can be explored further, exploring technical specifications, non-linear behaviors, and advanced applications.

For the interested reader, this may be the starting point of a longer and more detailed journey. Electronics offer endless possibilities for discovery, innovation and application. Whether designing new devices, improving existing technologies, or simply better understanding the technological world around us, there is always something new to learn and explore.

Invitation to learn more

I therefore invite the reader to continue exploring, studying and experimenting. Electronics is a discipline that combines theory and practice, requiring a deep understanding of its fundamental principles and an ability to apply these principles in real situations. Every project, every circuit and every component offers an opportunity to learn and grow.

I conclude with the hope that this article has sparked curiosity and interest in the field of electronics and that it can serve as a solid foundation for further exploration and discovery. The journey has just begun and the possibilities are endless.

Happy exploring!

Newsletter

If you want to be informed about the release of new articles, subscribe to the newsletter. Before subscribing to the newsletter read the page Privacy Policy (UE)

If you want to unsubscribe from the newsletter, click on the link that you will find in the newsletter email.