Introduction
Explore the world of audio by making a low pass op amp filter with adjustable cutoff frequency.
Introduce yourself to the exciting world of sound engineering, where total control of your audio experience becomes a reality! In this article, I’ll walk you through building a custom low-pass filter, a powerful and versatile device that lets you shape the sound quality to your desires. The distinctive feature of this project is the presence of two digital potentiometers, controlled by an ESP8266, which allow you to adjust the cutoff frequency of the filter.
The low pass filter is implemented with an operational amplifier in inverting configuration, a choice that simplifies the circuit as much as possible. But the real magic begins with the digital potentiometers, the intelligent heart of this system. Thanks to their connection to the ESP8266, you have the power to adjust the filter cutoff frequency in real time. Imagine being able to adapt your sound environment with a simple touch, customizing every aspect of the audio experience based on your tastes and needs.
This is not just a project for audiophiles, but opens doors to new possibilities in the world of digital synthesis. With such a powerful control element, you can easily integrate this low pass filter into your digital synthesizers, allowing for advanced customization of your sound repertoire. With this step-by-step guide, you’ll not only build your own low-pass filter, but you’ll also learn how to harness the full potential of digital technology to shape the sound to your liking. Get involved in the art of audio engineering and begin your journey in creating a bespoke sound environment.
What is an operational amplifier?
The operational amplifier (also called opamp) is a solid-state analog electronic component capable, as its name suggests, of amplifying an electrical signal. It is defined as operational because it is capable of carrying out some mathematical operations in a totally analogue manner on electrical signals. The generally possible operations are addition, subtraction, differentiation and integration, logarithm etc etc.
It is also a fundamental part of active low-pass, high-pass, band-pass, notch etc etc filters.
It is equipped with two inputs, one inverting (indicated with the – sign) and one non-inverting (indicated with the + sign), and one output. It is generally powered with a dual voltage (usually indicated with the signs V+ and V–).
In case the signal enters through the non-inverting input, the output signal is in the same phase as the input signal. If, however, the signal enters the inverting input, the output signal will be in phase opposition (i.e. 180 degrees out of phase) compared to the input signal.
An inverting amplifier is, therefore, an operational amplifier whose non-inverting input is connected to ground while the inverting one is connected to the VINPUT input source.
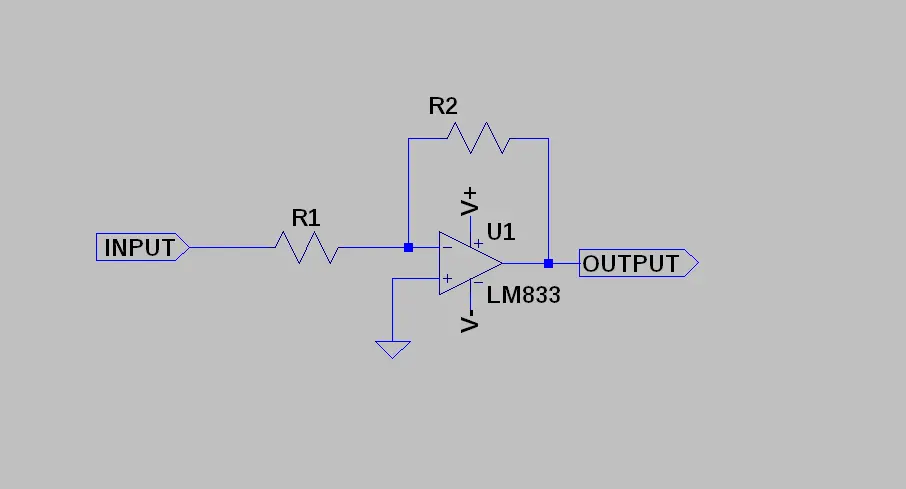
This circuit takes the signal at the INPUT terminal and presents it in the amplified OUTPUT (i.e. multiplied by a value called gain which we will indicate with the symbol G).
So, in formula, we have that:
VOUTPUT = G * VINPUTWe said that this amplifier inverts the phase of the output signal with respect to the phase of the input signal (the two signals are 180° out of phase). This means that the value of G is negative. For example, if the input signal were amplified 10 times, we would have G = -10 [V/V] and therefore:
VOUTPUT = -10 * VINPUTIf, for example, the signal VINPUT = 1V we would have VOUTPUT = -10 V while with VINPUT = -1 V we would have VOUTPUT = 10 V.
In practice the output signal is given by the input signal enlarged by 10 times and reversed.
PLEASE NOTE: the gain, being the ratio between two voltages
G = VOUTPUT / VINPUTit is expressed by a pure number. However, we can express it, alternatively, with the notation [V/V] (which is always a pure number).
How do you set the gain of the inverting amplifier?
The gain is easily determined starting from the values of the two resistors R1 and R2. In particular we have that the gain, in absolute value, is given by:
|G| = R2 / R1So, if we had R1 = 1 kΩ and R2 = 10 KΩ, we would have |G| = 10.
Considering the 180° phase shift we have that
G = -R2 / R1With the values of the previous example we have that G = -10 [V/V].
In other words:
VOUTPUT = -(R2 / R1) * VINPUTmeaning what:
VOUTPUT = -10 * VINPUTThe gain can also be expressed in dB (decibel) according to the relationship:
GdB = 20 * log(|G|) = 20 * log(|-R2 / R1|) = 20 * log (R2 / R1)For example, if R1 and R2 were 1 kΩ and 10 kΩ respectively, we would have G = -10 [V/V] and GdB = 20 dB. If R1 and R2 were 2 kΩ and 15 kΩ respectively, we would have G = -7.5 [V/V] and GdB = 17.5 dB.
How does a classic potentiometer work?
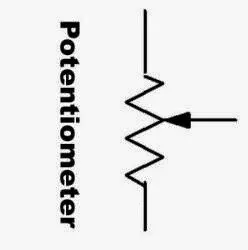
A potentiometer is a 3-terminal device used as a variable resistor. It is equipped with a rotary contact controlled by the knob and is used as a voltage divider.

Its electrical symbol is that of a classic resistor but with the intermediate contact controlled by the knob:
How does a voltage divider work?
A voltage divider is a simple circuit in which the output voltage is a fraction of the input voltage. Two fixed resistors or a potentiometer can be used.
Let’s see the scheme and formula:

The potentiometer is indicated with the letter P while R1 and R2 are the two sections of the total resistance which vary depending on the position of the cursor (which is controlled by the knob).
As you can see, the output voltage Vo is a fraction of the input voltage Vi. Vo varies between two extremes:
- Vo = 0 when R2 = 0 (the knob is turned all the way towards the terminal connected to the negative pole of the battery)
- Vo = Vi when R1 = 0 (the knob is turned all the way towards the terminal connected to the positive pole of the battery)
Digital potentiometers
These examples are based on mechanical potentiometers but there are also types of potentiometers on the market that are completely electronic and adjustable via an appropriate input signal. They are the so-called digital potentiometers.
Today we want to test one by controlling it via ESP8266, in particular the MCP41010 model, which is a single potentiometer. Its maximum value is 10 kΩ while the minimum value is around 100Ω.

Let’s now see the pinout of this component:

The name of the device depends on the maximum resistance value of the single digital potentiometer and the number of potentiometers present inside it. For example:
- MCP41010: single potentiometer, 10 kΩ
- MCP41050: single potentiometer, 50 kΩ
- MCP41100: single potentiometer, 100 kΩ
- MCP42010: two independent potentiometers, 10 kΩ
- MCP42050: two independent potentiometers, 50 kΩ
- MCP42100: two independent potentiometers, 100 kΩ
We will control our digital potentiometer through its SPI port appropriately driven by the ESP8266.
Looking at the datasheet of the digital potentiometer you can see how, to command this chip, it is necessary to first send it a “command byte” (to tell the chip what it must do) and then a “data byte” (to tell the chip what resistance value set, from 0 to 255).
For example, to set a resistance of 10 kΩ, we must send a data byte equal to 11111111 (corresponding to 255), to set a resistance of 5 kΩ we must send a data byte equal to 10000000 (corresponding to 128) and so on.
For the command to be executed, first the CS terminal must be set to 0 (LOW value) then the command byte must be sent followed by the data byte (for a total of 16 bits). Finally, you need to bring the CS terminal back to value 1 (HIGH value). Only then will the command be executed (from the datasheet:”Executing any command is accomplished by setting CS low and then clocking-in a command byte followed by a data byte into the 16-bit shift register. The command is executed when CS is raised.”)
We have already addressed the use of one of these digital potentiometers in the articles How to control a digital potentiometer using Arduino UNO and How to control an inverting operational amplifier using Arduino UNO and a digital potentiometer which I recommend you read.
Let’s start with a bit of theory
Linear Time Invariant Systems (SLTI)
The study of linear time invariant systems (SLTI) is fundamental in the field of electronic and control engineering, as it provides a systems approach to the analysis and design of dynamic systems. A system is considered LTI if it satisfies two fundamental properties: linearity and invariance over time. Linearity implies that the system respects the principle of superposition of effects, while invariance over time indicates that the response of the system does not change over time, as long as the input remains unchanged. Two common representations of such systems are the impulse response and the transfer function.
Impulse Response
The impulse response is a fundamental characteristic of an LTI dynamical system and is defined as the response of the system to a unit impulse, also known as the Dirac delta (denoted δ(t)). Therefore, if I place a Dirac impulse at the input of an SLTI system, I obtain the response of the system to that impulse, which I will indicate with the function h(t):

If h(t) is the impulse response of an LTI system, then the response y(t) of the system to any input x(t) can be obtained by computing the convolution between the input and the impulse response:

So, returning to the block diagrams, we will have that:

where the output y(t) is, as mentioned before, the convolution between the input x(t) and the impulse response h(t) (calculated with the integral above).
The convolution operation is indicated with the symbol * so we can write that y(t) = x(t) * h(t).
In essence, the impulse response h(t) of an SLTI is the function that characterizes the behavior of the system in the time domain.
Transfer Function
The transfer function, often denoted H(s) in the Laplace domain, is an alternative way of describing an LTI system. It represents the ratio between the Laplace transform of the response Y(s) and that of the input X(s). In practice it is the Laplace transform of the impulse response h(t):

Graphically we will represent our system like this:

The transfer function is useful because it simplifies the analysis of frequency systems. Just to give an example, convolution (not a very simple operation) transforms into a simple multiplication. So, in Laplace’s world we will have that the previous relation transforms into
Y(s) = X(s) H(s).
The poles (roots of the denominator) and zeros (roots of the numerator) of the transfer function provide crucial information about the stability and frequency response of the system.
The function H(s) is a function of a complex variable. In fact, the variable s, called Laplace variable, is a complex variable (i.e. with a real part and an imaginary part) and is represented as follows: s = α + jω (with real α and ω). For α = 0 we have s = jω. In this case the transfer function therefore depends only on the pulsation ω, i.e. we have H(ω) where the pulsation is linked to the frequency by the relation ω = 2πf. The magnitude and phase of H(ω) will be functions of ω. It therefore characterizes the behavior of the system in the frequency domain.
Frequency response of an SLTI
A key aspect of the study of LTI systems is the analysis of their frequency response. This analysis involves evaluating how the system responds to sinusoidal signals at different frequencies. The magnitude and phase of the transfer function are usually represented graphically via the Bode plot, providing a clear view of the attenuation and phase characteristics of the system as a function of frequency.
Brief theory of the low pass filter
A first-order low-pass filter is a simple electronic circuit or, more generally, a dynamic system characterized by a cutoff frequency that represents the point at which the signal begins to be attenuated. The transfer function H(s) of a first-order low-pass filter in the Laplace domain is expressed as:

where:
- K represents the static gain of the filter, i.e. the value of the gain when the frequency tends to zero.
- s is the complex variable of the Laplace transform
- T is the time constant of the system
The time constant T is inversely proportional to the cutoff frequency fc, and the relationship between them is given by:

The first order low pass filter acts like an RC circuit, where R is the resistance and C is the capacitance. The transfer function can also be written in the time domain as the impulsive response of the system h(t) (i.e. by calculating the anti-Laplace transform of the transfer function H(s)):

where:
- t is the time
- e is the base of the natural logarithm
The frequency response of the first-order low-pass filter means that it gradually attenuates frequencies above the cutoff frequency. This behavior can be visualized in the frequency domain through the Bode plot, where the magnitude of the transfer function decreases with a slope of -20 dB/decade, while the phase varies from 0° to -90°.
In general, the first-order low-pass filter finds wide use in several applications, including audio circuits, control systems, power electronics and more. Its simplicity makes it a popular choice for filtering signals with relatively low attenuation needs at higher frequencies.
The low pass filter made with an operational amplifier
As already seen, a low-pass filter is an electronic circuit designed to allow low-frequency signals to pass through while attenuating higher-frequency ones. This type of filter is fundamental in various audio and electronic applications, as it allows you to isolate and focus on the low frequency components of a signal. In the context of sound engineering, low pass filters are often used to eliminate or reduce unwanted frequencies and to focus on reproducing the deepest, most resonant tones of a sound. They are also essential in communications systems, where frequency separation is crucial to ensure clear, interference-free transmission. Due to their versatility, low-pass filters find use in a wide range of devices, from the design of audio speakers and amplifiers to the design of electronic signal processing circuits.
Obviously, in addition to low pass filters there are also high pass filters, band pass filters and band stop filters.
The cutoff frequency in a low pass filter is the critical point at which the filter begins to attenuate the frequencies of the signal. This is the frequency at which the signal begins to be reduced, and below this frequency the filter allows almost complete passage of low frequency components. In an ideal low-pass filter, above the cutoff frequency, the signal is attenuated gradually, eventually reaching a point where higher frequencies are dramatically reduced.
The cutoff frequency is a key parameter in the design of low pass filters, as it determines the range of frequencies that will be retained or attenuated. By adjusting the cutoff frequency, you can tailor the filter to the specific needs of your application, allowing precise control over the reproduction of frequencies in your audio or electronic signal. The correct setting of the cutoff frequency is essential to obtain the desired result in signal filtering.
A first-order low-pass filter can be made by using an operational amplifier in inverting configuration together with a reactive component, such as a capacitor. This type of filter is also known as a single-pole RC filter, since it involves only one reactive component. The typical configuration of a first-order low-pass filter with an operational amplifier is called a low-pass RC filter.
In RC low pass filter, the capacitor is connected between the inverting input of the op amp and its output. The resistor is connected to the inverting input and output terminal of the amplifier (in parallel with the capacitor). The cutoff frequency of the filter is determined by the relationship between the resistance (R) and the capacitance (C) according to the formula:
fc = 1/(2πRC)
Dove:
- fc is the cutoff frequency,
- R is the resistance,
- C is the capacity.
Below we see an example of a first order low pass filter created with an operational amplifier in inverting configuration:

In this particular case in which the resistances are equal, the voltage gain is equal to 1 [V/V] (equal to 0 dB) for frequencies sufficiently lower than the cutoff frequency fc and, as the frequency increases, it decreases gradually. This type of filter offers 20 dB/decade attenuation for input frequencies above the cutoff frequency.
The first-order low-pass filter configuration with operational amplifier offers a simple and effective solution to achieve smooth attenuation of high frequencies, and is widely used in audio and signal processing applications.
Let’s now look at some simulations performed with LTSpice which show us the behavior of the filter both in the frequency domain and in the time domain.
The circuit used is the following:

The V2 generator represents the 9V battery. The two resistors R5 and R6 divide the supply voltage (9V) to create a virtual ground. Therefore the junction of the two resistors is the ground of the circuit while the two dual supplies will be V+ = 4.5V and V– = -4.5V with respect to the virtual ground.
In this circuit the resistors R3 and R1 are indicated with {R}. This means that their value varies because it has been defined by a Spice directive i.e. .step param R 1k 10k 1k which says that the value of R starts from 1kΩ and reaches 10kΩ in steps of 1kΩ. Then 10 simulations are done, one for each value of R.
The resistors R4 and R2, equal to 10Ω, are placed for safety so that if in the real circuit the resistors R1 and R3 were to take on the value 0Ω, short circuits would not be created. With the current values we have as extreme values of the cut-off frequency:
- fc1 = 3388Hz for R = 1kΩ
- fc2= 338Hz for R = 10kΩ
The V3 generator generates a square wave with a frequency of 1kHz. So fc1 is far above the frequency of the input signal while fc2 is far below. From Fourier analysis we know that the square wave contains only odd harmonics. In the first case only the harmonics above approximately 3388Hz will be attenuated while in the second case all the harmonics, including the fundamental at 1kHz, will be attenuated.
Before seeing how this affects the output signal, let’s take a look at the Bode plot of the filter (as the value of R varies):

As can be seen, starting from around 300Hz all the curves, more or less, are starting to attenuate. In particular, the curve that attenuates the least (the green one at the top) is the one corresponding to fc1 for R = 1kΩ (at a frequency of 1kHz its attenuation is practically negligible) while the last one in violet, corresponding to fc2 for R = 10kΩ, is the one that attenuates the most. Already at a frequency of 1kHz it presents an attenuation of approximately 10dB.
Now let’s see how all this translates to our 1kHz square wave:

As you can see, in the lower half-plane we have the input square wave while in the upper half-plane we have the input square wave processed by the filter as the cut-off frequency varies.
The green wave, the one most similar to a true square wave, is the one corresponding to fc1. In the Bode plot we saw that there was a very small attenuation at 1 kHz and an attenuation of 3dB at the fc1 frequency. This attenuation means that the wave is not perfectly square because it has lost the harmonics above 3kHz and therefore presents itself with a rounded corner.
As the cutoff frequency is lowered towards fc2, more and more harmonics are attenuated and the signal, consequently, transforms significantly up to the last curve, the violet one, where it resembles a triangular wave.
So far the theory which I hope hasn’t been too boring!
Let’s move on to the practical part.
What components do we need for our low-pass op-amp filter with digital potentiometer?
To generate the square wave signal we need a signal generator. A simple model is more than enough.
Alternatively, you can also use the headphone output of your PC and use any audio software capable of generating a 1kHz square wave.
Project implementation
Before creating the actual circuit let’s take a look at the pinout of the board:

Let’s now see the Fritzing circuit diagram of the filter:

What we will do is inject a 500mVpp square wave signal at 1 kHz into the input and run a test sketch which, by acting on the digital potentiometers, will lower the filter cutoff frequency in steps. By connecting the output to an oscilloscope we will find a signal that varies like the one obtained following the simulation.
Optionally we can use (to hear the effect of the filter on the input signal) an amplifier module with LM386 and a 4/8 Ω speaker and at least 2/3 W.
Let’s now see the amplifier module with LM386:

The top connector is the power and signal input. The VDD terminal must be connected to the Vin terminal of the ESP8266 (which is at 5V), the GND terminals to the GND of the circuit while the IN terminal represents the input of the signal to be amplified (corresponding to pin 1 of the LM833)
The lower connector is connected to the speaker: the GND terminal to the black wire (or marked with “-“) of the speaker, the OUT terminal to the red wire (or marked with “+”).
This module is based on the LM386 integrated circuit, a low frequency power amplifier, capable of delivering a couple of W into a 4/8 Ω load.
Operating on a single 4V to 12V power supply, this amplifier IC is ideal for small-scale audio projects such as portable radios, audio interfaces and DIY projects. Some key features include:
- Adjustable Gain: the LM386 offers the ability to adjust gain through the use of external components. This feature allows customization of the amplification level based on the needs of the project.
- Low energy consumption: thanks to its low power consumption, the LM386 is suitable for battery-powered applications, contributing to the energy efficiency of devices.
- Simple Design: the LM386 simplifies the design process with a limited number of external components required for its operation. This aspect makes it particularly suitable for DIY projects and for those who are approaching audio circuit design for the first time.
The module we will use in this project contains an LM386 and a trimmer and is a pre-assembled audio amplifier, designed to simplify the integration of audio amplifiers into electronic projects. Features include:
- Integrated LM386: the module mounts the LM386 as the main component, providing a wide range of amplification possibilities for low-power audio signals.
- Adjustable Gain: the trimmer on the module allows the gain of the LM386 to be adjusted. This adjustment can be tailored to specific project needs, allowing precise control over the power of the amplified signal.
- Ease of use: thanks to the pre-assembled module, users can easily integrate audio amplification functionality into their designs without having to design the circuit from scratch.
- Power Flexibility: the module is designed to operate with a wide range of supply voltages, contributing to its versatility.
This module is particularly suitable for DIY audio projects, portable speakers, and other applications where low-power audio signals need to be amplified.
Let’s now see the Fritzing ectrical diagram of the filter with the amplifier module:

Note that there are 4 x 47nF capacitors. One is the filter’s own, connected between terminals 1 and 2 of the LM833. One, drawn on the left side of the ESP8266, is connected between the positive Vin line and ground to filter (clean up noise) this power supply. The other two are connected on one side to the ground and on the other respectively to the + and – pole of the 9 V battery to filter (clean up noise) also this dual power supply.
The sketch
Let’s create the PlatformIO project
We have already seen the procedure for creating a PlatformIO project in the article How to create a project for NodeMCU ESP8266 with PlatformIO.
Please do not install the libraries mentioned in the article as we will not be using any libraries.
Now edit the platformio.ini file to add these two lines:
monitor_speed = 115200
upload_speed = 921600
so that it looks like this:
[env:nodemcuv2]
platform = espressif8266
board = nodemcuv2
framework = arduino
monitor_speed = 115200
upload_speed = 921600
Obviously you can download the project from the following link:
Replace the main.cpp file of the project you created with the one present in the zip file.
Now let’s see how the sketch works.
We start by including the usual Arduino.h library:
#include <Arduino.h>
The GPIOs controlling the digital potentiometers are then defined:
int CS_signal = D2; // Chip Select signal on pin D2 of ESP8266
int CLK_signal = D4; // Clock signal on pin D4 of ESP8266
int MOSI_signal = D5; // MOSI signal on pin D5 of ESP8266
and the command byte (which we talked about in the paragraph dedicated to digital potentiometers) together with the initialization value:
byte cmd_byte2 = B00010001 ; // Command byte
int initial_value = 0; // Setting up the initial value
Three other parameters are then defined:
#define LOOP_DELAY 2000
#define RESISTANCE_STEP 30.5
double CAPACITY = 0.000000047;
The LOOP_DELAY is worth 2 seconds and is the interval between one step and another. Simply put we will lower the cutoff frequency of the filter every two seconds.
The CAPACITY is simply the value of the feedback capacitor (the 47nF one) expressed in Farads (we need it for calculating the cut-off frequency).
The RESISTANCE_STEP parameter is an experimental parameter. In reality, the maximum value measured on the MCP41010 digital potentiometers turned out to be different from 10kΩ (I measured them by placing the control value at its maximum, i.e. 255) but much closer to 7.8KΩ. So the resistance increase step is not given (at least in my case) by 10000Ω/256 i.e. approximately 39Ω but by 7800Ω/256 i.e. approximately 30.5Ω
Also try measuring the maximum value of the resistance of the digital potentiometer (sending it the value 255 via the SPI port) to see if it corresponds to the 10kΩ of the datasheet and then divide the value found by 256 in order to have the true value of RESISTANCE_STEP.
NOTE: it is obvious that if between the cursor of the digital potentiometer and one of the other two terminals the resistance value is maximum, between the cursor and the other terminal the value is zero (or almost zero).
Followed by the spi_transfer and spi_out functions which manage the transmission through the SPI port:
void spi_transfer(byte working) {
for(int i = 1; i <= 8; i++) { // Set up a loop of 8 iterations (8 bits in a byte)
if (working > 127) {
digitalWrite (MOSI_signal,HIGH) ; // If the MSB is a 1 then set MOSI high
} else {
digitalWrite (MOSI_signal, LOW) ; } // If the MSB is a 0 then set MOSI low
digitalWrite (CLK_signal,HIGH) ; // Pulse the CLK_signal high
working = working << 1 ; // Bit-shift the working byte
digitalWrite(CLK_signal,LOW) ; // Pulse the CLK_signal low
}
}
void spi_out(int CS, byte cmd_byte, byte data_byte){ // we need this function to send command byte and data byte to the chip
digitalWrite (CS, LOW); // to start the transmission, the chip select must be low
spi_transfer(cmd_byte); // send the COMMAND BYTE
delay(2);
spi_transfer(data_byte); // send the DATA BYTE
delay(2);
digitalWrite(CS, HIGH); // to stop the transmission, the chip select must be high
}
the initialize function that sends the initial value to the SPI port:
void initialize() { // send the command byte of value 0 (initial value)
spi_out(CS_signal, cmd_byte2, initial_value);
}
and the commandPotentiometer function used in the loop to impart the various step values and calculate the corresponding cutoff frequency actually set on the filter:
void commandPotentiometer(int step) {
spi_out(CS_signal, cmd_byte2, step);
Serial.print("step: ");
Serial.println(step);
Serial.print("approximate resistance value: ");
Serial.print(10 + (step * RESISTANCE_STEP));
Serial.println(" Ω");
Serial.print("approximate cutoff frequency value: ");
Serial.print(1/((10 + (step * RESISTANCE_STEP)) * 3.14 * 2 * CAPACITY));
Serial.println(" Hz");
Serial.println();
Serial.println();
}
Then we have the setup function:
void setup() {
pinMode (CS_signal, OUTPUT);
pinMode (CLK_signal, OUTPUT);
pinMode (MOSI_signal, OUTPUT);
initialize();
Serial.begin(115200); // setting the serial speed
Serial.println("ready!");
}
which initializes the GPIOs of the SPI port and defines them as OUTPUT, sets the initial value to send on the SPI bus and initializes the serial port.
In the loop function, the various commands are followed to set the current resistance value of the two digital potentiometers, increasing it so as to lower the filter cutoff frequency at each step:
int i = 2;
commandPotentiometer(i);
delay(LOOP_DELAY);
i = 8;
commandPotentiometer(i);
delay(LOOP_DELAY);
i = 12;
commandPotentiometer(i);
delay(LOOP_DELAY);
i = 30;
commandPotentiometer(i);
delay(LOOP_DELAY);
i = 45;
commandPotentiometer(i);
delay(LOOP_DELAY);
i = 64;
commandPotentiometer(i);
delay(LOOP_DELAY);
i = 96;
commandPotentiometer(i);
delay(LOOP_DELAY);
i = 128;
commandPotentiometer(i);
delay(LOOP_DELAY);
i = 160;
commandPotentiometer(i);
delay(LOOP_DELAY);
i = 192;
commandPotentiometer(i);
delay(LOOP_DELAY);
i = 224;
commandPotentiometer(i);
delay(LOOP_DELAY);
Now load the sketch, inject a 500mVpp square wave at 1 kHz into the input and connect the oscilloscope and/or amplifier module. If all goes well you should get a result like the one shown in the following video:
You will notice that two traces are represented on the oscilloscope: the light blue one is the input (i.e. the signal coming from the signal generator i.e. a square wave with an amplitude equal to 500 mVpp and a frequency equal to 1 kHz) while the yellow one is the output .
You will notice that at the beginning (step 2) this trace looks a lot like a square wave and, in particular, to the input one (with the only difference that they have inverted phase since, as you will remember, the operational amplifier is in an inverting configuration ). They are very similar because in this case, since the resistance of the digital potentiometers is very low, the cut-off frequency is much greater than 1 kHz, therefore only a few harmonics are blocked/attenuated by the filter. As we proceed with the steps, the resistance increases, consequently the cut-off frequency decreases and therefore the number of harmonics of the square wave blocked/attenuated by the filter increases, with the consequent modification of the waveform of the signal output that increasingly resembles a triangular wave. As well as visually, this behavior can also be felt via the speaker as the timbre of the sound (as well as its amplitude) changes.
Adding a remote control
We therefore tested the filter with the test sketch which however does not leave us much freedom to control it at will. We can then exploit the ESP8266’s ability to connect to WiFi and be controlled via REST APIs. This allows us to insert our filter into a larger and more complex system where modules of this kind are controlled and set in real time by special programs in order to generate different effects. We have already covered the topic of REST APIs in the How to build a REST API server with ESP32 article so I recommend you go and take a look at it. Even if we talk about ESP32 there, the conceptual basis does not change.
As already highlighted in the aforementioned article, REST APIs are a way to make different devices communicate with each other or to allow us to interact with each other. With the second sketch that we will use in this article we will create a web server with the ESP8266 so that it exposes a set of REST APIs. We can use these REST APIs to interact with the ESP8266 in order to receive data from the filter or send data to the filter. In particular we will send the value between 0 and 255 to set the resistance of the two digital potentiometers with a POST and we will obtain the resistance value set on the digital potentiometers and the value of the cut-off frequency via a GET.
The GET type API will look like this:
http://IP_ESP8266/getValues
and will send a Json file like this as a response:
{
"cutoffFrequency": "56874",
"cutoffResistance": "4850"
}
where IP_ESP8266 is the IP address assigned to the board by the router, cutoffFrequency represents the value of the calculated cutoff frequency while cutoffResistance represents the value of the resistance presented by the two digital potentiometers.
The POST type API looks like this:
http://IP_ESP8266/setCutoffFrequency
and it will send a Json file like this to our ESP8266:
{
"resistanceCode": "156"
}
where IP_ESP8266 is the IP address assigned to the board by the router and resistanceCode represents the value between 0 and 255 to set the resistance of the two digital potentiometers.
To interact with the ESP8266 via the REST API we will use a program called Postman, whose use we will see later.
Also for this example we will create the project using the PlatformIO IDE.
Then create a new project with PlatformIO, download the following project file:
Unzip it and replace the main.cpp file and the platformio.ini file of the newly created project with those present in the downloaded and unzipped project.
The platformio.ini file will look like this:
[env:nodemcuv2]
platform = espressif8266
board = nodemcuv2
framework = arduino
monitor_speed = 115200
upload_speed = 921600
lib_deps =
bblanchon/ArduinoJson@^6.21.0
https://github.com/tzapu/WiFiManager.git
Let’s look at this sketch now. It is based on the previous one. Furthermore there is the management of the WiFi connection and the REST API, so I won’t dwell on the parts already covered previously.
Initially the necessary libraries are included:
#include <Arduino.h>
#include <ESP8266WebServer.h>
#include <ArduinoJson.h>
#include <WiFiManager.h>
The variables
unsigned long measureDelay = 500; // 0.5 seconds
unsigned long lastTimeRan;
that decide how often the loop function must control the digital potentiometers are then defined.
Subsequently, the server listening on port 80 is instantiated, a Json document is defined, a 1024 character buffer and the variable that will contain the code (between 0 and 255) that will set the resistances of the digital potentiometers:
// Web server running on port 80
ESP8266WebServer server(80);
StaticJsonDocument<1024> jsonDocument;
char buffer[1024];
int resistanceCode = 0;
The handlePost function follows which manages the POST type API:
void handlePost() {
if (server.hasArg("plain") == false) {
//handle error here
}
String body = server.arg("plain");
deserializeJson(jsonDocument, body);
// Get code for resistance
resistanceCode = jsonDocument["resistanceCode"];
// Respond to the client
server.send(200, "application/json", "{}");
}
and the createJson, addJsonObject, getValues functions which manage the Json document and return, following a GET request, the cutoffFrequency and cutoffResistance values:
void createJson(char *name, float value, char *unit) {
jsonDocument.clear();
jsonDocument["name"] = name;
jsonDocument["value"] = value;
jsonDocument["unit"] = unit;
serializeJson(jsonDocument, buffer);
}
void addJsonObject(char *name, float value, char *unit) {
JsonObject obj = jsonDocument.createNestedObject();
obj["name"] = name;
obj["value"] = value;
obj["unit"] = unit;
}
void getValues() {
Serial.println("Get all values");
jsonDocument.clear(); // Clear json buffer
addJsonObject("cutoffFrequency", cutoffFrequency, "Hz");
addJsonObject("cutoffResistance", cutoffResistance, "Ω");
serializeJson(jsonDocument, buffer);
server.send(200, "application/json", buffer);
}
The setupApi function follows which routes the /getValues and /setCutoffFrequency urls to the appropriate functions and initializes the server:
void setupApi() {
server.on("/getValues", getValues);
server.on("/setCutoffFrequency", HTTP_POST, handlePost);
// start server
server.begin();
}
The setup function also has the following part:
WiFi.mode(WIFI_STA); // explicitly set mode, esp defaults to STA+AP
// it is a good practice to make sure your code sets wifi mode how you want it.
//WiFiManager, Local intialization. Once its business is done, there is no need to keep it around
WiFiManager wm;
// reset settings - wipe stored credentials for testing
// these are stored by the esp library
// wm.resetSettings();
// Automatically connect using saved credentials,
// if connection fails, it starts an access point with the specified name ( "AutoConnectAP"),
// if empty will auto generate SSID, if password is blank it will be anonymous AP (wm.autoConnect())
// then goes into a blocking loop awaiting configuration and will return success result
bool res;
// res = wm.autoConnect(); // auto generated AP name from chipid
// res = wm.autoConnect("AutoConnectAP"); // anonymous ap
res = wm.autoConnect("AutoConnectAP","password"); // password protected ap
if(!res) {
Serial.println("Failed to connect");
ESP.restart();
}
else {
//if you get here you have connected to the WiFi
Serial.println("Connected...yeey :)");
}
setupApi();
which takes care of managing the WiFi connection and calls the setupApi() function.
The loop function handles client calls from the server and, every measureDelay seconds, calls the commandPotentiometer(resistanceCode) function which sets the value contained in resistanceCode (received from the POST API):
server.handleClient();
if (millis() > lastTimeRan + measureDelay) {
commandPotentiometer(resistanceCode);
lastTimeRan = millis();
}
How to connect the board to the Internet
After uploading the sketch to the board, open the Serial Monitor to see the messages coming from the device.
First the board goes into Access Point mode and will provide us with an IP address that we will use shortly. This operation is used to connect the board to the Internet without having to enter the WiFi network parameters (SSID and password) in the code.

In this case the IP address is 192.168.4.1.
At this point the ESP8266 is in Access Point mode (with AutoConnectAP SSID) and we need to connect our computer to the AutoConnectAP network. If we go to the networks menu of our computer, we should also see the AutoConnectAP network in the list of wireless networks.

Connect your computer to the AutoConnectAP network. Then go to your browser and enter the IP previously provided by the ESP8266 (which in this example is 192.168.4.1)
You will see a screen like this:

Click the ConfigureWiFi button. It will show you the available networks:

Choose your network’s SSID:

Enter your network password and click the save button:


The ESP8266 module keeps the access parameters stored even if you turn it off, it will remember them when restarting and will automatically reconnect without having to repeat this procedure. Only if you reset it by uncommenting this line
// wm.resetSettings();
will lose the connection parameters.
Please note: the device can only memorize one network. If you later connect it to another network, it will forget the settings of the previous network.
Let’s test the project with REST APIs
Once the ESP8266 has been connected to the WiFi network it will provide us with its IP address via the PlatformIO Serial Monitor, as visible in the following figure:

In this case the IP assigned by the router to the board is 192.168.1.9. This IP will be used to compose the REST API.
To interact with the board we need special software called Postman. After installing the program, we are ready to use it.
This is what its home screen looks like:

In the main window there is a bar where you will need to enter the API.
To the left of this bar there is a drop-down menu that allows you to choose the type of API (for example GET, POST, PUT…).
Now choose the POST type and enter the POST API that will have the following format:
192.168.1.8/setCutoffFrequency
PLEASE NOTE: in subsequent experiments the IP 192.168.1.8 was assigned so the following images will refer to this IP.
Obviously you will have to enter the IP address assigned to your ESP8266.
Before pressing the Send button, you will need to select the Body item which is under the URL bar. Then select the raw item (under Body) and then, on the drop-down menu on the right, select the JSON item instead of Text, as shown in the photo:

In the window below enter the Json:
{
"resistanceCode": "128"
}
This is what the Postman window should look like:

Press the Send button to send the Json with the resistanceCode parameter. By varying the value of the resistanceCode parameter (between 0 and 255) you will vary the resistance of the digital potentiometers and, consequently, the cutoff frequency of the filter. The closer the resistanceCode gets to 255, the lower the cutoff frequency is.
To see the current state of the filter (i.e. to see what resistance has been set and, consequently, what cutoff frequency) now choose the GET type and enter the GET API that will have formed:
http://IP_ESP8266/getValues
For example, in this case, since the assigned IP is 192.168.1.8, the API URL will be:
http://192.168.1.8/getValues
Obviously you will have to enter the IP address assigned to your ESP8266.
Press the Send button on the right.
The API will return a Json file reporting the detected cutoffFrequency and cutoffResistance values, as shown in the following image:

Final remarks
You were able to see how to interact with the ESP8266 via the REST API and therefore vary the filter cutoff frequency. To do this you used the Postman program. But you could also interact in another way, such as with a Python script that queries the board automatically via the REST API. Therefore having a program that interacts, giving commands or receiving data, in a completely autonomous and independent manner.
But these commands can also be given by another device such as another ESP8266 (or an ESP32 or any other suitable device), thus creating real communication between devices (without manual intervention on our part).
If you are a guitarist and want to apply this filter, or rather a slightly more advanced version, I advise you to read the article DIY guitar distortion effect pedal with ESP8266: construction, use and adjustment to create a personalized speaker.
Newsletter
If you want to be informed about the release of new articles, subscribe to the newsletter. Before subscribing to the newsletter read the page Privacy Policy (UE)
If you want to unsubscribe from the newsletter, click on the link that you will find in the newsletter email.
🔗 Follow us on our social channels so you don’t miss any updates!
📢 Join our Telegram channel to receive real-time updates.
🐦 Follow us on Twitter to always stay informed about our news.
Thank you for being part of our TechRM community! 🚀